2025년 2월 11일
Exploring the Limit of Outcome Reward for Learning Mathematical Reasoning
(Chengqi Lyu, Songyang Gao, Yuzhe Gu, Wenwei Zhang, Jianfei Gao, Kuikun Liu, Ziyi Wang, Shuaibin Li, Qian Zhao, Haian Huang, Weihan Cao, Jiangning Liu, Hongwei Liu, Junnan Liu, Songyang Zhang, Dahua Lin, Kai Chen)
Reasoning abilities, especially those for solving complex math problems, are crucial components of general intelligence. Recent advances by proprietary companies, such as o-series models of OpenAI, have made remarkable progress on reasoning tasks. However, the complete technical details remain unrevealed, and the techniques that are believed certainly to be adopted are only reinforcement learning (RL) and the long chain of thoughts. This paper proposes a new RL framework, termed OREAL, to pursue the performance limit that can be achieved through Outcome REwArd-based reinforcement Learning for mathematical reasoning tasks, where only binary outcome rewards are easily accessible. We theoretically prove that behavior cloning on positive trajectories from best-of-N (BoN) sampling is sufficient to learn the KL-regularized optimal policy in binary feedback environments. This formulation further implies that the rewards of negative samples should be reshaped to ensure the gradient consistency between positive and negative samples. To alleviate the long-existing difficulties brought by sparse rewards in RL, which are even exacerbated by the partial correctness of the long chain of thought for reasoning tasks, we further apply a token-level reward model to sample important tokens in reasoning trajectories for learning. With OREAL, for the first time, a 7B model can obtain 94.0 pass@1 accuracy on MATH-500 through RL, being on par with 32B models. OREAL-32B also surpasses previous 32B models trained by distillation with 95.0 pass@1 accuracy on MATH-500. Our investigation also indicates the importance of initial policy models and training queries for RL. Code, models, and data will be released to benefit future research https://github.com/InternLM/OREAL.
Binary Feedback 상황에서 BoN 샘플이 KL penalized Optimal Policy 학습에 충분하다는 것을 기반으로, Negative 샘플을 고려한 Reward shaping과 단순한 Token level reward model을 사용한 학습.
KL penalty를 사용한다고 생각하면 BoN과 연결하는 것은 자연스럽죠. 그런 의미에서 RL CoT 문제에 대해서 KL penalty의 효과를 이해하는 것이 중요하다고 생각합니다.
Training RL CoT model based on the principle that BoN sampling is sufficient for training a KL-penalized optimal policy in binary feedback situations. The approach incorporates reward shaping for negative samples and utilizes a simple token-level reward model for training.
It's natural to connect RL with BoN when using KL penalties. In this context, I believe it's crucial to understand the effects of KL penalties on RL CoT tasks.
#reasoning #rl
On the Emergence of Thinking in LLMs I: Searching for the Right Intuition
(Guanghao Ye, Khiem Duc Pham, Xinzhi Zhang, Sivakanth Gopi, Baolin Peng, Beibin Li, Janardhan Kulkarni, Huseyin A. Inan)
Recent AI advancements, such as OpenAI's new models, are transforming LLMs into LRMs (Large Reasoning Models) that perform reasoning during inference, taking extra time and compute for higher-quality outputs. We aim to uncover the algorithmic framework for training LRMs. Methods like self-consistency, PRM, and AlphaZero suggest reasoning as guided search. We ask: what is the simplest, most scalable way to enable search in LLMs? We propose a post-training framework called Reinforcement Learning via Self-Play (RLSP). RLSP involves three steps: (1) supervised fine-tuning with human or synthetic demonstrations of the reasoning process, (2) using an exploration reward signal to encourage diverse and efficient reasoning behaviors, and (3) RL training with an outcome verifier to ensure correctness while preventing reward hacking. Our key innovation is to decouple exploration and correctness signals during PPO training, carefully balancing them to improve performance and efficiency. Empirical studies in the math domain show that RLSP improves reasoning. On the Llama-3.1-8B-Instruct model, RLSP can boost performance by 23% in MATH-500 test set; On AIME 2024 math problems, Qwen2.5-32B-Instruct improved by 10% due to RLSP. However, a more important finding of this work is that the models trained using RLSP, even with the simplest exploration reward that encourages the model to take more intermediate steps, showed several emergent behaviors such as backtracking, exploration of ideas, and verification. These findings demonstrate that RLSP framework might be enough to enable emergence of complex reasoning abilities in LLMs when scaled. Lastly, we propose a theory as to why RLSP search strategy is more suitable for LLMs inspired by a remarkable result that says CoT provably increases computational power of LLMs, which grows as the number of steps in CoT [LLZM24, MS23]. Our code is available at:
https://github.com/
GuanghaoYe/Emergence-of-Thinking.
RL CoT. SFT, Exploration을 추구하는 RL의 결합. (Exploration을 증가시키기 위해 Length Reward(!)를 사용했네요.)
중간에 다음 단계로 새로운 것을 창조하는 능력을 언급하고 있군요. 저도 창조성이 다음 목표가 되지 않을까 싶습니다.
RL CoT. A combination of SFT, RL pursuing exploration. (Interestingly, they used length reward (!) to increase exploration.)
They mention that the next step for RL CoT would be developing the ability to create new things. I also think creativity might be the next focus for LLMs.
#reasoning #rl
The Curse of Depth in Large Language Models
(Wenfang Sun, Xinyuan Song, Pengxiang Li, Lu Yin, Yefeng Zheng, Shiwei Liu)
In this paper, we introduce the Curse of Depth, a concept that highlights, explains, and addresses the recent observation in modern Large Language Models(LLMs) where nearly half of the layers are less effective than expected. We first confirm the wide existence of this phenomenon across the most popular families of LLMs such as Llama, Mistral, DeepSeek, and Qwen. Our analysis, theoretically and empirically, identifies that the underlying reason for the ineffectiveness of deep layers in LLMs is the widespread usage of Pre-Layer Normalization (Pre-LN). While Pre-LN stabilizes the training of Transformer LLMs, its output variance exponentially grows with the model depth, which undesirably causes the derivative of the deep Transformer blocks to be an identity matrix, and therefore barely contributes to the training. To resolve this training pitfall, we propose LayerNorm Scaling, which scales the variance of output of the layer normalization inversely by the square root of its depth. This simple modification mitigates the output variance explosion of deeper Transformer layers, improving their contribution. Our experimental results, spanning model sizes from 130M to 1B, demonstrate that LayerNorm Scaling significantly enhances LLM pre-training performance compared to Pre-LN. Moreover, this improvement seamlessly carries over to supervised fine-tuning. All these gains can be attributed to the fact that LayerNorm Scaling enables deeper layers to contribute more effectively during training.
Pre LN에서 레이어의 기여도가 낮아지는 문제에 대한 답. 레이어 번호로 크기를 조정하는 것은 종종 시도되는 방법이었는데 여기서는 블록의 출력 레이어가 아니라 Pre LN의 출력을 축소시켰군요.
MiniMax-01에서는 아예 DeepNorm을 썼죠. (https://arxiv.org/abs/2501.08313, https://arxiv.org/abs/2203.00555) 늘 재미있는 주제이긴 합니다.
This paper offers a solution to the problem of Pre LN reducing the contribution of deeper layers. While scaling based on layer index has been attempted before, this paper takes a different approach by scaling the output of Pre LN, rather than the output layer of the blocks.
MiniMax-01 took a different route by using DeepNorm to address this issue. (https://arxiv.org/abs/2501.08313, https://arxiv.org/abs/2203.00555) This remains an interesting area of research.
#normalization #transformer
MATH-Perturb: Benchmarking LLMs' Math Reasoning Abilities against Hard Perturbations
(Kaixuan Huang, Jiacheng Guo, Zihao Li, Xiang Ji, Jiawei Ge, Wenzhe Li, Yingqing Guo, Tianle Cai, Hui Yuan, Runzhe Wang, Yue Wu, Ming Yin, Shange Tang, Yangsibo Huang, Chi Jin, Xinyun Chen, Chiyuan Zhang, Mengdi Wang)
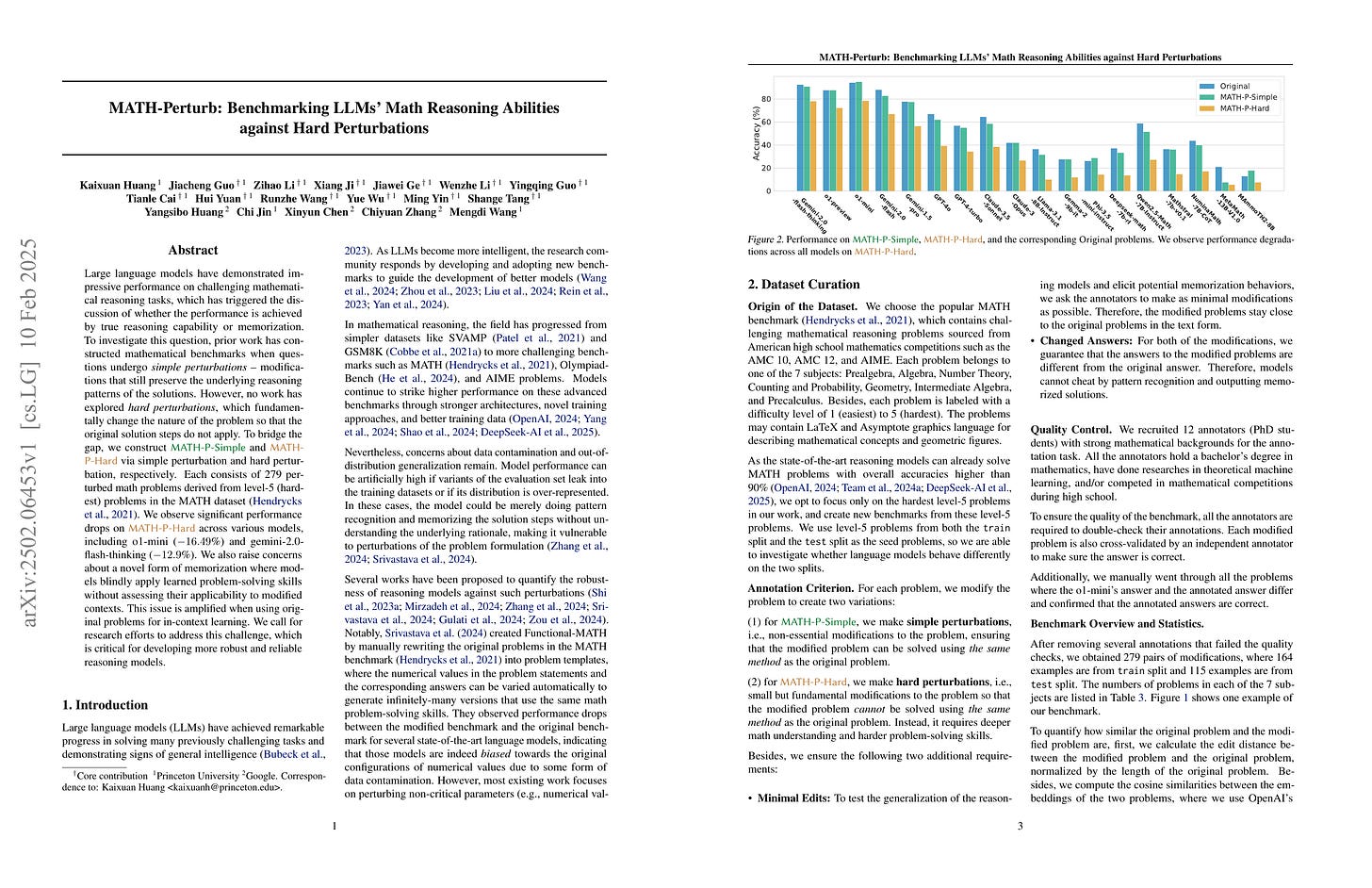
Large language models have demonstrated impressive performance on challenging mathematical reasoning tasks, which has triggered the discussion of whether the performance is achieved by true reasoning capability or memorization. To investigate this question, prior work has constructed mathematical benchmarks when questions undergo simple perturbations -- modifications that still preserve the underlying reasoning patterns of the solutions. However, no work has explored hard perturbations, which fundamentally change the nature of the problem so that the original solution steps do not apply. To bridge the gap, we construct MATH-P-Simple and MATH-P-Hard via simple perturbation and hard perturbation, respectively. Each consists of 279 perturbed math problems derived from level-5 (hardest) problems in the MATH dataset (Hendrycksmath et. al., 2021). We observe significant performance drops on MATH-P-Hard across various models, including o1-mini (-16.49%) and gemini-2.0-flash-thinking (-12.9%). We also raise concerns about a novel form of memorization where models blindly apply learned problem-solving skills without assessing their applicability to modified contexts. This issue is amplified when using original problems for in-context learning. We call for research efforts to address this challenge, which is critical for developing more robust and reliable reasoning models.
MATH의 문제를 바꿔 원 문제를 푸는 방식으로는 풀 수 없게 만들어서 모델을 테스트해봤군요. 생각보다 모델들이 강인하네요.
Benchmark made by perturbing the MATH problems so that they couldn't be solved using the method of solution for the original problems. The models seem more robust than expected.
#benchmark
μnit Scaling: Simple and Scalable FP8 LLM Training
(Saaketh Narayan, Abhay Gupta, Mansheej Paul, Davis Blalock)
Large Language Model training with 8-bit floating point (FP8) formats promises significant efficiency improvements, but reduced numerical precision makes training challenging. It is currently possible to train in FP8 only if one is willing to tune various hyperparameters, reduce model scale, or accept the overhead of computing dynamic scale factors. We demonstrate simple, scalable FP8 training that requires no dynamic scaling factors or special hyperparameters, even at large model sizes. Our method, μnit Scaling (μS), also enables simple hyperparameter transfer across model widths, matched numerics across training and inference, and other desirable properties. μnit Scaling is straightforward to implement, consisting of a set of minimal interventions based on a first-principles analysis of common transformer operations. We validate our method by training models from 1B to 13B parameters, performing all hidden linear layer computations in FP8. We achieve quality equal to higher precision baselines while also training up to 33% faster.
가변 Scaling factor 없이 FP8 학습을 하기 위한 방법.
A method for FP8 training without dynamic scaling factors.
#efficient-training
Can 1B LLM Surpass 405B LLM? Rethinking Compute-Optimal Test-Time Scaling
(Runze Liu, Junqi Gao, Jian Zhao, Kaiyan Zhang, Xiu Li, Biqing Qi, Wanli Ouyang, Bowen Zhou)
Test-Time Scaling (TTS) is an important method for improving the performance of Large Language Models (LLMs) by using additional computation during the inference phase. However, current studies do not systematically analyze how policy models, Process Reward Models (PRMs), and problem difficulty influence TTS. This lack of analysis limits the understanding and practical use of TTS methods. In this paper, we focus on two core questions: (1) What is the optimal approach to scale test-time computation across different policy models, PRMs, and problem difficulty levels? (2) To what extent can extended computation improve the performance of LLMs on complex tasks, and can smaller language models outperform larger ones through this approach? Through comprehensive experiments on MATH-500 and challenging AIME24 tasks, we have the following observations: (1) The compute-optimal TTS strategy is highly dependent on the choice of policy model, PRM, and problem difficulty. (2) With our compute-optimal TTS strategy, extremely small policy models can outperform larger models. For example, a 1B LLM can exceed a 405B LLM on MATH-500. Moreover, on both MATH-500 and AIME24, a 0.5B LLM outperforms GPT-4o, a 3B LLM surpasses a 405B LLM, and a 7B LLM beats o1 and DeepSeek-R1, while with higher inference efficiency. These findings show the significance of adapting TTS strategies to the specific characteristics of each task and model and indicate that TTS is a promising approach for enhancing the reasoning abilities of LLMs.
PRM과 탐색을 사용한 최적 Inference-time Scaling 방법 탐색. PRM이 일반화가 잘 되지 않는다는 문제를 여기서도 지적하고 있고, 이 일반화 문제 때문에 최적 탐색 전략 또한 PRM에 따라 변화하는군요.
This paper explores optimal inference-time scaling methods using PRM and search. It also highlights the generalization problem of PRMs, noting that this generalization issue causes the optimal search strategy to vary depending on the PRM used.
#inference-time-scaling #reward-model
Large Language Models Meet Symbolic Provers for Logical Reasoning Evaluation
(Chengwen Qi, Ren Ma, Bowen Li, He Du, Binyuan Hui, Jinwang Wu, Yuanjun Laili, Conghui He)
First-order logic (FOL) reasoning, which involves sequential deduction, is pivotal for intelligent systems and serves as a valuable task for evaluating reasoning capabilities, particularly in chain-of-thought (CoT) contexts. Existing benchmarks often rely on extensive human annotation or handcrafted templates, making it difficult to achieve the necessary complexity, scalability, and diversity for robust evaluation. To address these limitations, we propose a novel framework called ProverGen that synergizes the generative strengths of Large Language Models (LLMs) with the rigor and precision of symbolic provers, enabling the creation of a scalable, diverse, and high-quality FOL reasoning dataset, ProverQA. ProverQA is also distinguished by its inclusion of accessible and logically coherent intermediate reasoning steps for each problem. Our evaluation shows that state-of-the-art LLMs struggle to solve ProverQA problems, even with CoT prompting, highlighting the dataset's challenging nature. We also finetune Llama3.1-8B-Instruct on a separate training set generated by our framework. The finetuned model demonstrates consistent improvements on both in-distribution and out-of-distribution test sets, suggesting the value of our proposed data generation framework. Code available at: https://github.com/opendatalab/ProverGen
1차 술어 논리 문제들을 생성하기 위한 프레임워크. 논리 문제는 문제 생성이 가능한 영역이죠. 다만 논리학 냄새가 좀 덜 나게 만들 수 있는 방법이 있을까도 문제가 될 것 같네요.
A framework for generating first-order predicate logic problems. Logic problems are an area where problem generation is feasible. Maybe it would be better if we can find ways to make the problems feel less like formal logic.
#synthetic-data #reasoning
Dynamic Loss-Based Sample Reweighting for Improved Large Language Model Pretraining
(Daouda Sow, Herbert Woisetschläger, Saikiran Bulusu, Shiqiang Wang, Hans-Arno Jacobsen, Yingbin Liang)
Pretraining large language models (LLMs) on vast and heterogeneous datasets is crucial for achieving state-of-the-art performance across diverse downstream tasks. However, current training paradigms treat all samples equally, overlooking the importance or relevance of individual samples throughout the training process. Existing reweighting strategies, which primarily focus on group-level data importance, fail to leverage fine-grained instance-level information and do not adapt dynamically to individual sample importance as training progresses. In this paper, we introduce novel algorithms for dynamic, instance-level data reweighting aimed at improving both the efficiency and effectiveness of LLM pretraining. Our methods adjust the weight of each training sample based on its loss value in an online fashion, allowing the model to dynamically focus on more informative or important samples at the current training stage. In particular, our framework allows us to systematically devise reweighting strategies deprioritizing redundant or uninformative data, which we find tend to work best. Furthermore, we develop a new theoretical framework for analyzing the impact of loss-based reweighting on the convergence of gradient-based optimization, providing the first formal characterization of how these strategies affect convergence bounds. We empirically validate our approach across a spectrum of tasks, from pretraining 7B and 1.4B parameter LLMs to smaller-scale language models and linear regression problems, demonstrating that our loss-based reweighting approach can lead to faster convergence and significantly improved performance.
Loss Reweighting을 통한 LM 학습 개선. Learnability (https://arxiv.org/abs/2310.15389, https://arxiv.org/abs/2404.07965) 계통의 연구들이 생각나는데 학습 중인 모델 자체의 Loss 통계만으로 잘 작동할지 궁금하네요.
Improving LM training through loss reweighting. This reminds me of learnability-related research (https://arxiv.org/abs/2310.15389, https://arxiv.org/abs/2404.07965). I'm curious whether it would work effectively using only the loss statistics of the model being trained.
#pretraining