2024년 2월 15일
Transformers Can Achieve Length Generalization But Not Robustly
(Yongchao Zhou, Uri Alon, Xinyun Chen, Xuezhi Wang, Rishabh Agarwal, Denny Zhou
)
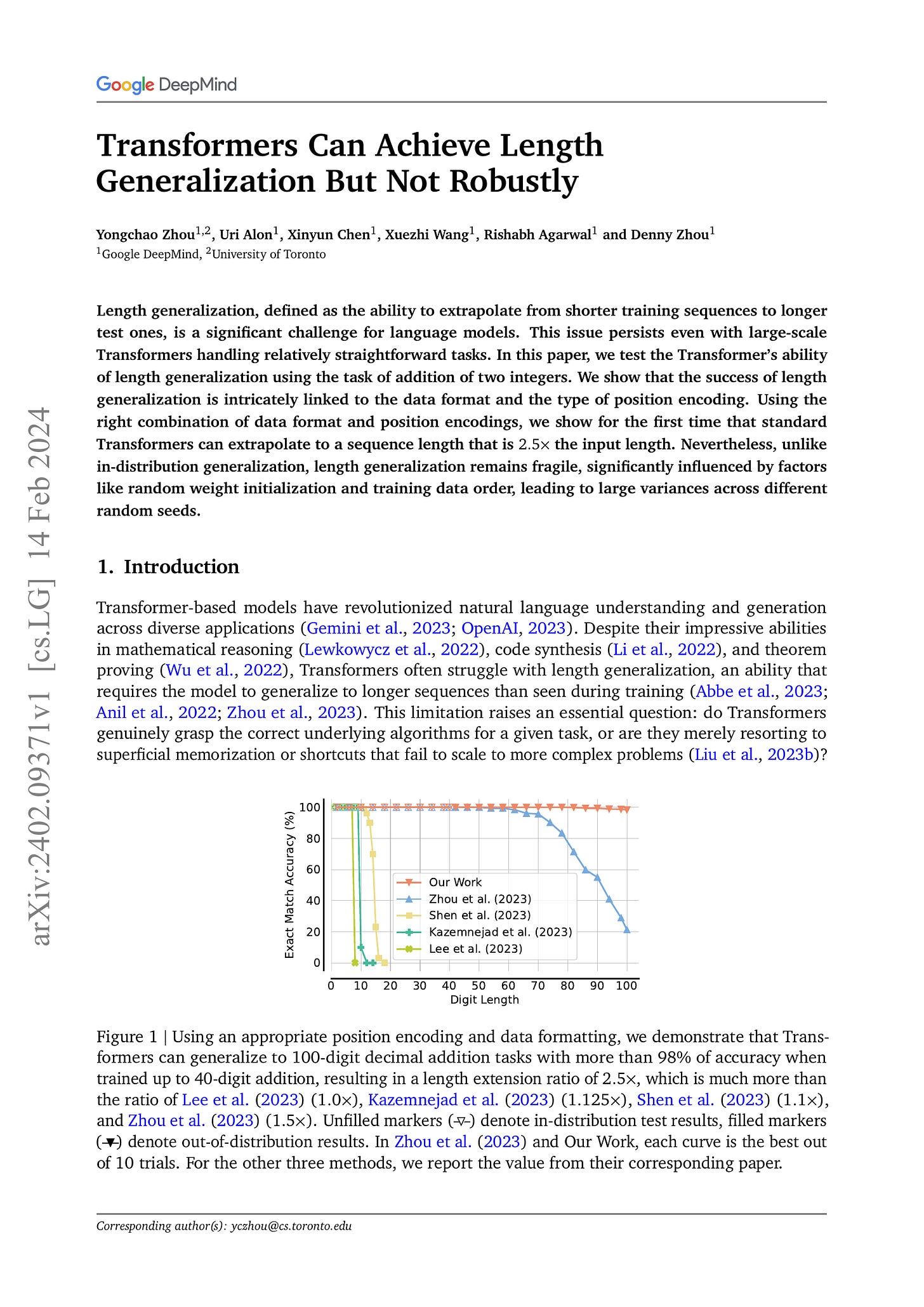
Length generalization, defined as the ability to extrapolate from shorter training sequences to longer test ones, is a significant challenge for language models. This issue persists even with large-scale Transformers handling relatively straightforward tasks. In this paper, we test the Transformer's ability of length generalization using the task of addition of two integers. We show that the success of length generalization is intricately linked to the data format and the type of position encoding. Using the right combination of data format and position encodings, we show for the first time that standard Transformers can extrapolate to a sequence length that is 2.5x the input length. Nevertheless, unlike in-distribution generalization, length generalization remains fragile, significantly influenced by factors like random weight initialization and training data order, leading to large variances across different random seeds.
트랜스포머의 Length Generalization 연구. 덧셈에 대해서 테스트했는데 FIRE (https://arxiv.org/abs/2310.04418), 숫자 순서 뒤집기, 자릿수에 대한 힌트, 거기에 추가적으로 Randomized PE (https://arxiv.org/abs/2305.16843) 까지 더했습니다. 사실 Randomized PE를 쓰면 테스트 분포의 PE까지 들어오기 때문에 좀 반칙이 아닌가 싶긴 하네요.
그렇지만 이 모든 트릭을 결합해도 Weight의 초기화 시드나 학습 데이터의 순서에 따라 성능이 크게 달라지는군요. Length Generalization은 운이 좋으면 나타나는 특성으로 보입니다.
Positional Encoding은 대칭성에 관한 문제일 것이고 숫자의 순서를 뒤집는다거나 하는 것은 Causal LM의 특성과 관련된 문제겠죠. 아직 이에 대한 확실한 해법이 없네요.
#transformer #long-context
Mitigating Reward Hacking via Information-Theoretic Reward Modeling
(Yuchun Miao, Sen Zhang, Liang Ding, Rong Bao, Lefei Zhang, Dacheng Tao)
Despite the success of reinforcement learning from human feedback (RLHF) in aligning language models with human values, reward hacking, also termed reward overoptimization, remains a critical challenge, which primarily stems from limitations in reward modeling, i.e., generalizability of the reward model and inconsistency in the preference dataset. In this work, we tackle this problem from an information theoretic-perspective, and propose a generalizable and robust framework for reward modeling, namely InfoRM, by introducing a variational information bottleneck objective to filter out irrelevant information and developing a mechanism for model complexity modulation. Notably, we further identify a correlation between overoptimization and outliers in the latent space, establishing InfoRM as a promising tool for detecting reward overoptimization. Inspired by this finding, we propose the Integrated Cluster Deviation Score (ICDS), which quantifies deviations in the latent space, as an indicator of reward overoptimization to facilitate the development of online mitigation strategies. Extensive experiments on a wide range of settings and model scales (70M, 440M, 1.4B, and 7B) support the effectiveness of InfoRM. Further analyses reveal that InfoRM's overoptimization detection mechanism is effective, potentially signifying a notable advancement in the field of RLHF. Code will be released upon acceptance.
Reward Modeling에 Information Bottleneck을 결합시켰군요. 추가로 Overoptimization을 Reward Model의 Information Bottleneck을 사용해 탐지하는 방법을 제안합니다. 클러스터링으로 SFT와 RLHF의 분포의 괴리를 탐지하는 방법이네요.
앞으로도 Reward Overoptimization은 인기 있는 주제일 것 같습니다. 최근 연구들은 보면 기존 딥 러닝 업계에서 Generalization이나 Noisy Label 문제에 대해 시도했던 방법들을 꺼내와서 시도해보고 있다는 느낌이 있네요.
#reward-model #regularization
Premise Order Matters in Reasoning with Large Language Models
(Xinyun Chen, Ryan A. Chi, Xuezhi Wang, Denny Zhou)
Large language models (LLMs) have accomplished remarkable reasoning performance in various domains. However, in the domain of reasoning tasks, we discover a frailty: LLMs are surprisingly brittle to the ordering of the premises, despite the fact that such ordering does not alter the underlying task. In particular, we observe that LLMs achieve the best performance when the premise order aligns with the context required in intermediate reasoning steps. For example, in deductive reasoning tasks, presenting the premises in the same order as the ground truth proof in the prompt (as opposed to random ordering) drastically increases the model's accuracy. We first examine the effect of premise ordering on deductive reasoning on a variety of LLMs, and our evaluation shows that permuting the premise order can cause a performance drop of over 30%. In addition, we release the benchmark R-GSM, based on GSM8K, to examine the ordering effect for mathematical problem-solving, and we again observe a significant drop in accuracy, relative to the original GSM8K benchmark.
전제의 순서가 바뀌면 LLM의 추론 성능이 바뀐다는 결과. 즉 A -> B, B -> C 순서일 때가 B -> C, A -> B 순서일 때보다 성능이 낫다는 것이네요. Reversal Curse (https://arxiv.org/abs/2309.12288) 가 떠오르네요.
#llm