2024년 11월 7일
How Transformers Solve Propositional Logic Problems: A Mechanistic Analysis
(Guan Zhe Hong, Nishanth Dikkala, Enming Luo, Cyrus Rashtchian, Rina Panigrahy)
Large language models (LLMs) have shown amazing performance on tasks that require planning and reasoning. Motivated by this, we investigate the internal mechanisms that underpin a network's ability to perform complex logical reasoning. We first construct a synthetic propositional logic problem that serves as a concrete test-bed for network training and evaluation. Crucially, this problem demands nontrivial planning to solve, but we can train a small transformer to achieve perfect accuracy. Building on our set-up, we then pursue an understanding of precisely how a three-layer transformer, trained from scratch, solves this problem. We are able to identify certain "planning" and "reasoning" circuits in the network that necessitate cooperation between the attention blocks to implement the desired logic. To expand our findings, we then study a larger model, Mistral 7B. Using activation patching, we characterize internal components that are critical in solving our logic problem. Overall, our work systemically uncovers novel aspects of small and large transformers, and continues the study of how they plan and reason.
트랜스포머가 명제 논리를 해결하기 위해 사용하는 회로 분석. Mistral 7B로 실험한 것이 꽤 재미있네요. 쿼리와 관련된 규칙을 찾는 헤드, 수집한 쿼리와 규칙 정보를 응답 위치로 옮기는 헤드, 사실을 처리하는 헤드, 그리고 최종 결정을 하는 헤드로 구성되어 있군요. 이런 구조가 형성된다는 것이 새삼 신기하긴 합니다.
Analysis of the circuits transformers use to solve propositional logic. The experiment with Mistral 7B is quite interesting. It consists of heads that find rules related to the query, heads that move collected query and rule information to the response position, heads that process facts, and heads that make the final decision. It's still fascinating to see how such a structure forms from the next token prediction.
#mechanistic-interpretation
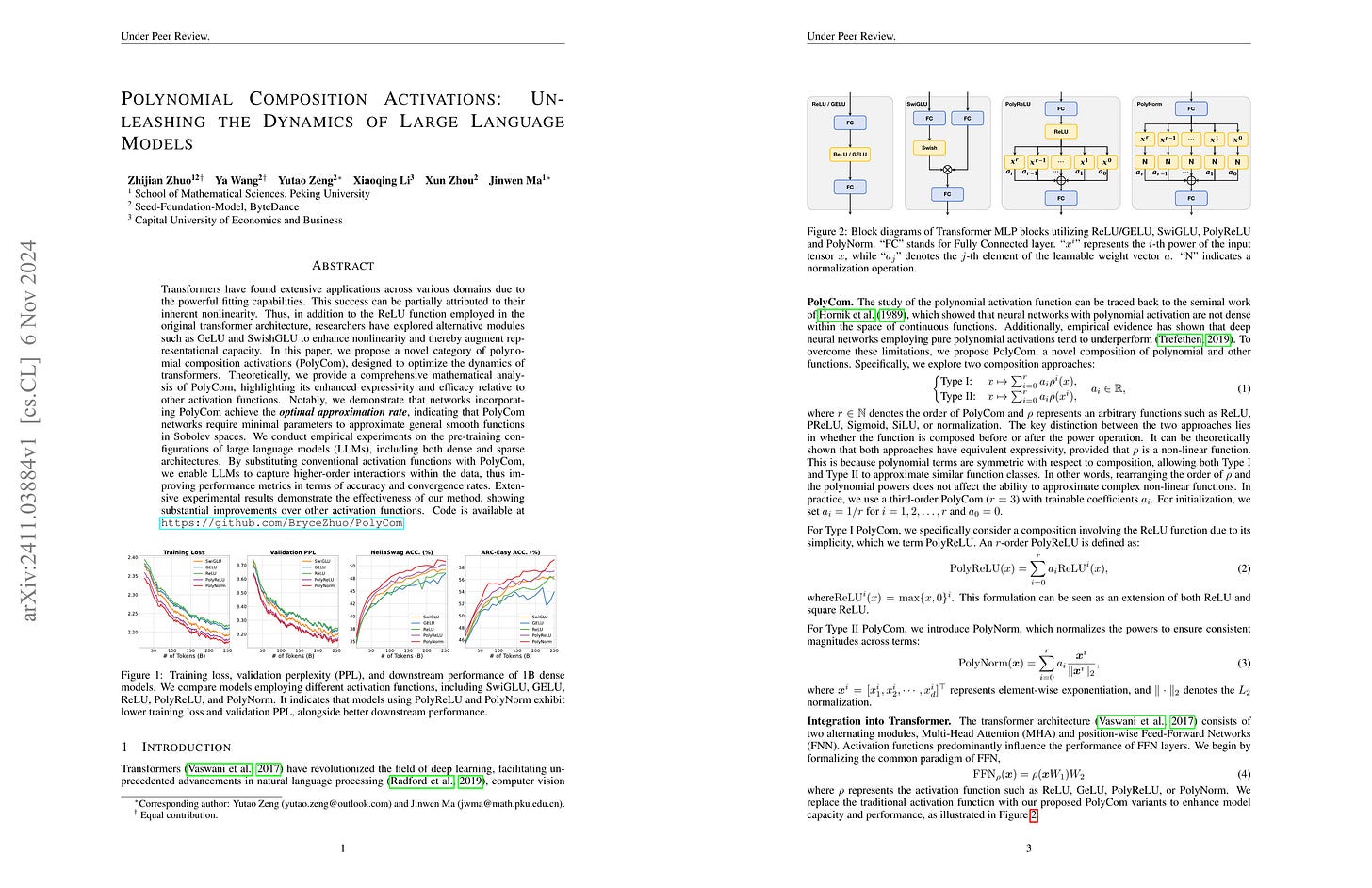
Polynomial Composition Activations: Unleashing the Dynamics of Large Language Models
(Zhijian Zhuo, Ya Wang, Yutao Zeng, Xiaoqing Li, Xun Zhou, Jinwen Ma)
Transformers have found extensive applications across various domains due to the powerful fitting capabilities. This success can be partially attributed to their inherent nonlinearity. Thus, in addition to the ReLU function employed in the original transformer architecture, researchers have explored alternative modules such as GeLU and SwishGLU to enhance nonlinearity and thereby augment representational capacity. In this paper, we propose a novel category of polynomial composition activations (PolyCom), designed to optimize the dynamics of transformers. Theoretically, we provide a comprehensive mathematical analysis of PolyCom, highlighting its enhanced expressivity and efficacy relative to other activation functions. Notably, we demonstrate that networks incorporating PolyCom achieve the optimal approximation rateoptimal approximation rate, indicating that PolyCom networks require minimal parameters to approximate general smooth functions in Sobolev spaces. We conduct empirical experiments on the pre-training configurations of large language models (LLMs), including both dense and sparse architectures. By substituting conventional activation functions with PolyCom, we enable LLMs to capture higher-order interactions within the data, thus improving performance metrics in terms of accuracy and convergence rates. Extensive experimental results demonstrate the effectiveness of our method, showing substantial improvements over other activation functions. Code is available at https://github.com/BryceZhuo/PolyCom.
비선형 함수의 다항식으로 구성한 Activation 함수. Activation과 Optimizer는 건드리지 말라는 것이 딥 러닝 판의 오랜 격언이긴 했습니다만...SwiGLU 같은 Activation도 절찬리에 사용되고 있다는 것을 고려하면 속도에 큰 손해가 없으면 쓸 수도 있겠다 싶긴 합니다.
An activation function composed of polynomials of nonlinear functions. While there's been a long-standing wisdom in deep learning not to tinker with activations and optimizers, considering the widespread success of activations like SwiGLU, it seems this approach could be viable if it doesn't significantly compromise speed.
#activation #transformer
LASER: Attention with Exponential Transformation
(Sai Surya Duvvuri, Inderjit S. Dhillon)
Transformers have had tremendous impact for several sequence related tasks, largely due to their ability to retrieve from any part of the sequence via softmax based dot-product attention. This mechanism plays a crucial role in Transformer's performance. We analyze the gradients backpropagated through the softmax operation in the attention mechanism and observe that these gradients can often be small. This poor gradient signal backpropagation can lead to inefficient learning of parameters preceeding the attention operations. To this end, we introduce a new attention mechanism called LASER, which we analytically show to admit a larger gradient signal. We show that LASER Attention can be implemented by making small modifications to existing attention implementations. We conduct experiments on autoregressive large language models (LLMs) with upto 2.2 billion parameters where we show upto 3.38% and an average of ~1% improvement over standard attention on downstream evaluations. Using LASER gives the following relative improvements in generalization performance across a variety of tasks (vision, text and speech): 4.67% accuracy in Vision Transformer (ViT) on Imagenet, 2.25% error rate in Conformer on the Librispeech speech-to-text and 0.93% fraction of incorrect predictions in BERT with 2.2 billion parameters.
Attention 확률이 대부분 0에 가깝기 때문에 발생하는 그래디언트의 감소를 해소. log(softmax(QK^T)exp(V)) 형태입니다.
This method addresses the issue of gradient reduction caused by most attention probabilities being close to zero. It takes the form of log(softmax(QK^T)exp(V)).
#transformer
Number Cookbook: Number Understanding of Language Models and How to Improve It
(Haotong Yang, Yi Hu, Shijia Kang, Zhouchen Lin, Muhan Zhang)
Large language models (LLMs) can solve an increasing number of complex reasoning tasks while making surprising mistakes in basic numerical understanding and processing (such as 9.11 > 9.9). The latter ability is essential for tackling complex arithmetic and mathematical problems and serves as a foundation for most reasoning tasks, but previous work paid little attention to it or only discussed several restricted tasks (like integer addition). In this paper, we comprehensively investigate the numerical understanding and processing ability (NUPA) of LLMs. Firstly, we introduce a benchmark covering four common numerical representations and 17 distinct numerical tasks in four major categories, resulting in 41 meaningful combinations in total. These tasks are derived from primary and secondary education curricula, encompassing nearly all everyday numerical understanding and processing scenarios, and the rules of these tasks are very simple and clear. Through the benchmark, we find that current LLMs fail frequently in many of the tasks. To study the problem, we train small models with existing and potential techniques for enhancing NUPA (such as special tokenizers, PEs, and number formats), comprehensively evaluating their effectiveness using our testbed. We also finetune practical-scale LLMs on our proposed NUPA tasks and find that 1) naive finetuning can improve NUPA a lot on many but not all tasks, and 2) surprisingly, techniques designed to enhance NUPA prove ineffective for finetuning pretrained models. We further explore the impact of chain-of-thought techniques on NUPA. Our work takes a preliminary step towards understanding and improving NUPA of LLMs. Our benchmark and code are released at https://github.com/GraphPKU/number_cookbook.
9.11 > 9.9 같은 숫자와 관련된 LLM의 문제들을 테스트하기 위한 과제들을 구성하고 토크나이저나 포맷 등이 미치는 영향, 그리고 파인튜닝으로 성능을 개선할 수 있는지를 분석. 결론적으로 토크나이저 등의 변경이 도움이 된다, 파인튜닝으로 성능을 올릴 수 있지만 한계가 있다, CoT 튜닝이 좀 더 도움이 된다는군요.
The authors designed tasks to test LLMs' numerical reasoning problems, which would catch common mistakes of LLMs like 9.11 > 9.9. They analyzed the effects of various tokenizer choices and number formats, as well as whether performance could be improved through fine-tuning. Their conclusions are, modifying tokenizers and formats is beneficial, fine-tuning can improve performance but has limitations, and CoT tuning proves to be more helpful.
#llm #benchmark #reasoning
Cosmos Tokenizer: A suite of image and video neural tokenizers
(Fitsum Reda, Jinwei Gu, Xian Liu, Songwei Ge, Ting-Chun Wang, Haoxiang Wang, Ming-Yu Liu)
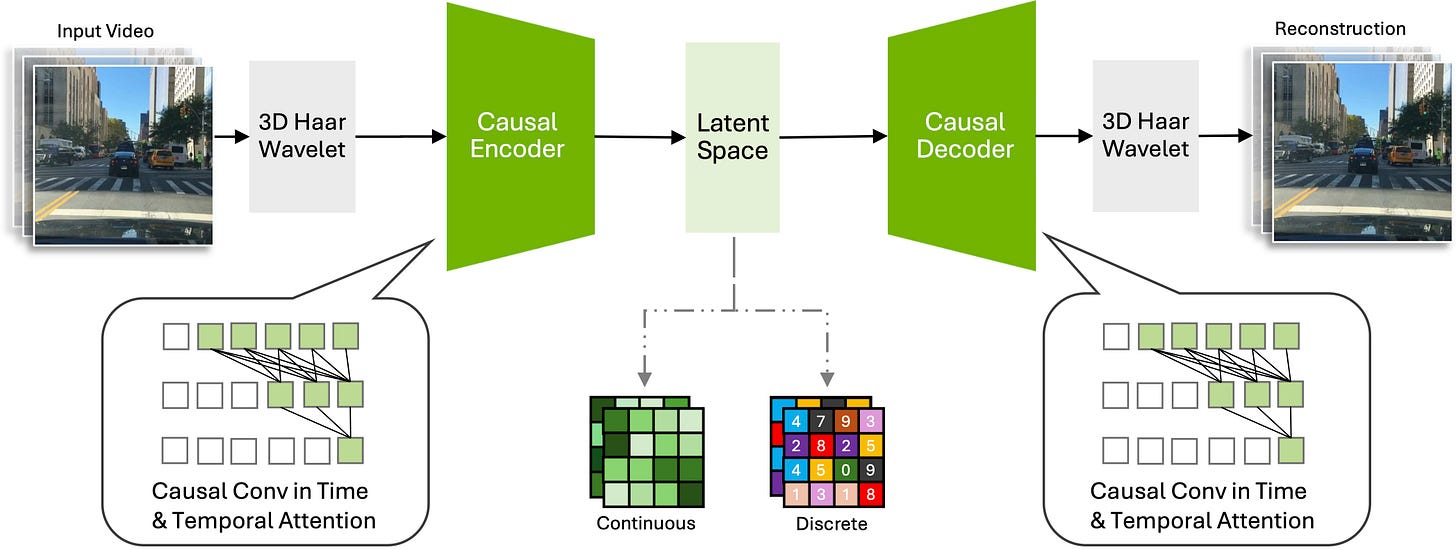
We present Cosmos Tokenizer, a suite of image and video tokenizers that advances the state-of-the-art in visual tokenization, paving the way for scalable, robust and efficient development of large auto-regressive transformers (such as LLMs) or diffusion generators. This repo hosts the inference codes and shares pre-trained models for the different tokenizers. Please check out our demo video.
NVIDIA의 이미지/비디오 토크나이저. 64K FSQ Discrete Token 혹은 KL 페널티 없는 바닐라 오토인코더를 사용한 Continuous Token. 비디오의 시간축에 대해서는 Causal합니다. CNN 기반으로 웨이블릿 공간에서 작동하는군요. Perceptual, Optical Flow, Gram Matrix Loss 사용까지. 굉장히 고전적인 맛의 모델이네요.
NVIDIA's image/video tokenizer. It uses 64K FSQ discrete tokens or continuous tokens using a vanilla autoencoder without KL penalty. It's causal along the temporal axis for videos. It's CNN-based and operates in wavelet space. Also the authors have used perceptual, optical flow, and gram matrix losses. A very classical taste of approach.
#tokenizer #vq